[ planet-factor ]

John Benediktsson: Cosine FizzBuzz

After revisiting FizzBuzz yesterday to discuss a Lazy FizzBuzz using infinite lazy lists, I thought I would not return to the subject for awhile. Apparently, I was wrong!

Susam Pal just wrote a really fun article about Solving Fizz Buzz with Cosines:

We define a set of four functions { s0, s1, s2, s3 } for integers n by:

s0(n) = n

s1(n) = Fizz

s2(n) = Buzz

s3(n) = FizzBuzz

And from that, they derive a formula which is essentially a finite Fourier series for computing the nth value in the FizzBuzz sequence, showing a nice fixed periodic cycling across n mod 15, resolving at each value of n to either the integers 0, 1, 2, 3:

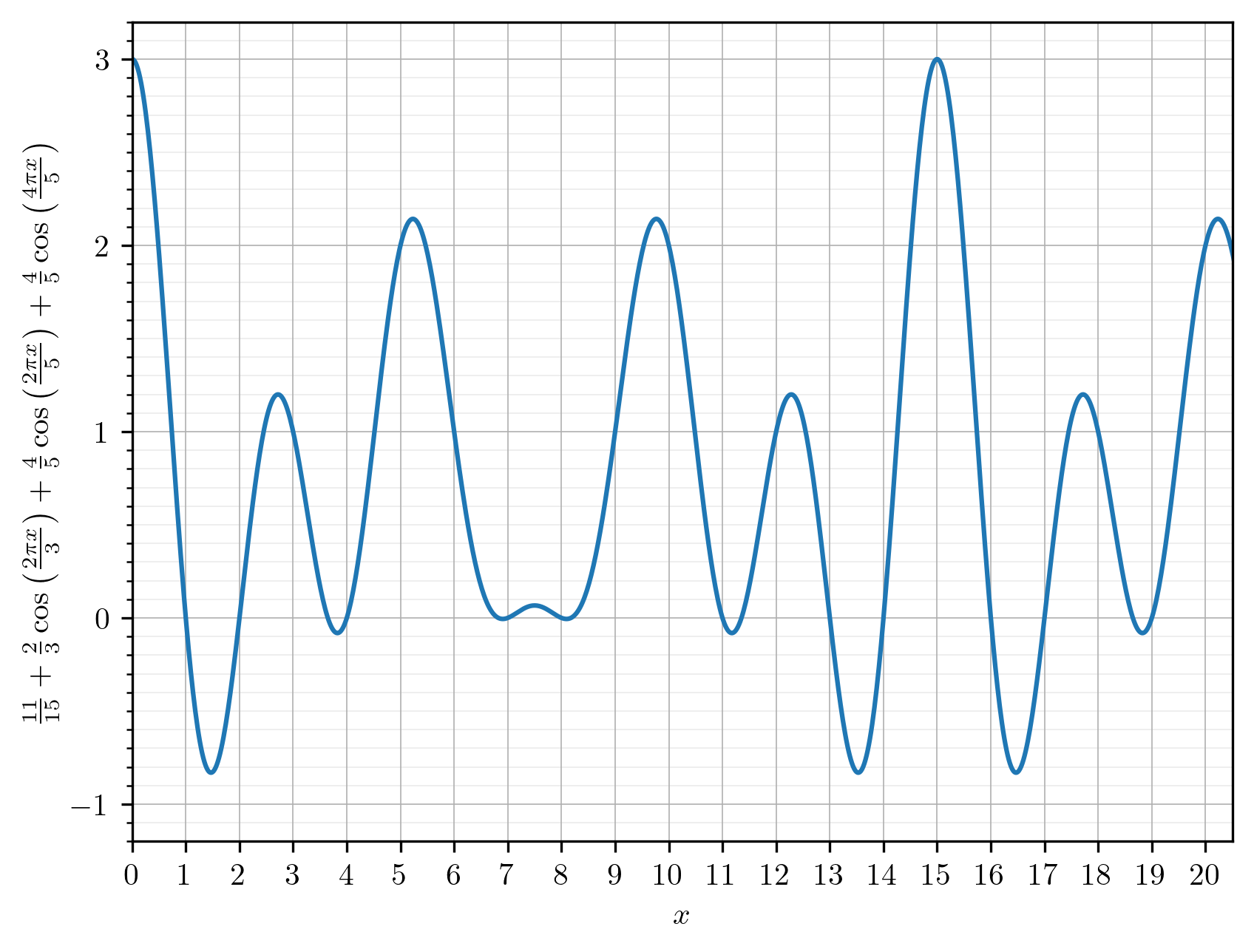
I recommend reading the whole article, but I will jump to an implementation of the formula in Factor:

:: fizzbuzz ( n -- val )
    11/15
    2/3 n * pi * cos 2/3 * +
    2/5 n * pi * cos 4/5 * +
    4/5 n * pi * cos + round >integer
    { n "Fizz" "Buzz" "FizzBuzz" } nth ;

And we can use that to compute the first few values in the sequence:

IN: scratchpad 1 ..= 100 [ fizzbuzz . ] each
1
2
"Fizz"
4
"Buzz"
"Fizz"
7
8
"Fizz"
"Buzz"
11
"Fizz"
13
14
"FizzBuzz"
16
17
"Fizz"
19
"Buzz"
...

Or, even some arbitrary values in the sequence:

IN: scratchpad 67 fizzbuzz .
67

IN: scratchpad 9,999,999 fizzbuzz .
"Fizz"

IN: scratchpad 10,000,000 fizzbuzz .
"Buzz"

IN: scratchpad 1,234,567,890 fizzbuzz .
"FizzBuzz"

Thats even more fun than using lazy lists!

Sat, 22 Nov 2025 15:00:00

John Benediktsson: Lazy FizzBuzz

I wrote about FizzBuzz many years ago. It’s a silly programming task often cited and even included on RosettaCode. The task is described as:

Write a program that prints the integers from 1 to 100 (inclusive).

But:

for multiples of three, print "Fizz" instead of the number;

for multiples of five, print "Buzz" instead of the number;

for multiples of both three and five, print "FizzBuzz" instead of the number.

This has been solved ad nauseum, but a few days ago Evan Hawn wrote about solving Fizz Buzz without conditionals or booleans using Python and the itertools.cycle function to create an infinitely iterable solution.

Let’s build this in Factor!

There are several ways to implement this, including generators, but we will be using the lists.lazy vocabulary to provide a lazy and infinite stream of values. In particular, by combining a stream of integers with a cycle of "Fizz" and a cycle of "Buzz".

The lists.circular vocabulary extends circular sequences to support the lists protocol:

IN: scratchpad USE: lists.circular

IN: scratchpad { 1 2 3 } <circular> 10 ltake list>array .
{ 1 2 3 1 2 3 1 2 3 1 }

Using that, we can create an infinite FizzBuzz list:

: lfizzbuzz ( -- list )
    1 lfrom
    { "" "" "Fizz" } <circular>
    { "" "" "" "" "Buzz" } <circular>
    lzip [ concat ] lmap-lazy lzip ;

We can print out the first few values quite simply:

IN: scratchpad lfizzbuzz 20 ltake [ first2 "%2d: %s\n" printf ] leach
 1:
 2:
 3: Fizz
 4:
 5: Buzz
 6: Fizz
 7:
 8:
 9: Fizz
10: Buzz
11:
12: Fizz
13:
14:
15: FizzBuzz
16:
17:
18: Fizz
19:
20: Buzz

And if we wanted a more traditional stream alternating between numbers and labels:

IN: scratchpad lfizzbuzz 100 ltake [ first2 [ nip ] unless-empty . ] leach
1
2
"Fizz"
4
"Buzz"
"Fizz"
7
8
"Fizz"
"Buzz"
11
"Fizz"
13
14
"FizzBuzz"
16
17
"Fizz"
19
"Buzz"
...

While not the ultimate FizzBuzz Enterprise Edition, this seems like a fun way to improve upon the simple meant for whiteboards implementation that is most often shared.

Fri, 21 Nov 2025 15:00:00

John Benediktsson: Lorem Ipsum

Lorem ipsum is a type of placeholder text that can be used in graphic design or web development. The most common form of it will often begin like this paragraph:

Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.

I wanted to make a program to generate believable lorem ipsum text using Factor.

We start by defining a bunch of possible words:

CONSTANT: words qw{
    a ab accusamus accusantium ad adipisci alias aliquam aliquid
    amet animi aperiam architecto asperiores aspernatur
    assumenda at atque aut autem beatae blanditiis commodi
    consectetur consequatur consequuntur corporis corrupti culpa
    cum cumque cupiditate debitis delectus deleniti deserunt
    dicta dignissimos distinctio dolor dolore dolorem doloremque
    dolores doloribus dolorum ducimus ea eaque earum eius
    eligendi enim eos error esse est et eum eveniet ex excepturi
    exercitationem expedita explicabo facere facilis fuga fugiat
    fugit harum hic id illo illum impedit in incidunt inventore
    ipsa ipsam ipsum iste itaque iure iusto labore laboriosam
    laborum laudantium libero magnam magni maiores maxime minima
    minus modi molestiae molestias mollitia nam natus
    necessitatibus nemo neque nesciunt nihil nisi nobis non
    nostrum nulla numquam obcaecati odio odit officia officiis
    omnis optio pariatur perferendis perspiciatis placeat porro
    possimus praesentium provident quae quaerat quam quas quasi
    qui quia quibusdam quidem quis quisquam quo quod quos
    ratione recusandae reiciendis rem repellat repellendus
    reprehenderit repudiandae rerum saepe sapiente sed sequi
    similique sint sit soluta sunt suscipit tempora tempore
    temporibus tenetur totam ullam unde ut vel velit veniam
    veritatis vero vitae voluptas voluptate voluptatem
    voluptates voluptatibus voluptatum
}

We then use these to build a random ipsum sentence:

: random-sentence ( -- str )
    2 ..= 5 random [
        words 3 ..= 12 random sample " " join
    ] replicate ", " join
    0 over [ ch>upper ] change-nth "?." random suffix ;

Then build a random ipsum paragraph from sentences:

: random-paragraph ( -- str )
    2 ..= 4 random [ random-sentence ] replicate " " join ;

We can define the initial paragraph above:

CONSTANT: initial-paragraph "\
Lorem ipsum dolor sit amet, consectetur adipisicing \
elit, sed do eiusmod tempor incididunt ut labore et \
dolore magna aliqua. Ut enim ad minim veniam, quis \
nostrud exercitation ullamco laboris nisi ut aliquip ex \
ea commodo consequat. Duis aute irure dolor in \
reprehenderit in voluptate velit esse cillum dolore eu \
fugiat nulla pariatur. Excepteur sint occaecat cupidatat \
non proident, sunt in culpa qui officia deserunt mollit \
anim id est laborum."

And use it to make random ipsum paragraphs, starting with the initial one:

: random-paragraphs ( n -- str )
    <iota> [
        zero? [ initial-paragraph ] [ random-paragraph ] if
    ] map "\n" join ;

Or even generate a list of random ipsum words, understanding that sample can’t generate more samples than the length of the sequence being sampled from:

:: random-words ( n -- str )
    words length :> w
    [
        n [ words over w min sample % w [-] ] until-zero
    ] { } make ;

We can make a command-line interface using the argument parser to return words, sentence, or paragraph:

CONSTANT: OPTIONS {
    T{ option
        { name "--w" }
        { help "Generate some lorem ipsum words" }
        { #args 1 }
        { type integer }
    }
    T{ option
        { name "--s" }
        { help "Generate a lorem ipsum sentence" }
        { const t }
        { default f }
    }
    T{ option
        { name "--p" }
        { help "Generate a lorem ipsum paragraph" }
        { const t }
        { default f }
    }
}

MAIN: [
    OPTIONS [
        "w" get [ random-words print ] when*
        "s" get [ random-sentence print ] when
        "p" get [ random-paragraph print ] when
    ] with-options
]

And that gives you automatic help text showing the available options:

$ ./factor -run=lorem-ipsum --help
Usage:
    factor -run=lorem-ipsum [--help] [--w W] [--s] [--p]

Options:
    --help    show this help and exit
    --w W     Generate some lorem ipsum words
    --s       Generate a lorem ipsum sentence
    --p       Generate a lorem ipsum paragraph

We can test it by generating some words, a sentence, and a paragraph:

$ ./factor -run=lorem-ipsum --w 10
vero eos quos optio magni soluta nulla delectus voluptas neque

$ ./factor -run=lorem-ipsum --s
Totam dicta laborum perferendis unde voluptas, culpa dignissimos odio
distinctio rem eius, tempora harum corporis accusamus.

$ ./factor -run=lorem-ipsum --p
Quaerat maiores veniam minus reprehenderit architecto numquam mollitia earum,
natus assumenda eius cumque minima sint magni accusantium facere, eius aperiam
explicabo molestias voluptatibus aspernatur maiores assumenda, nulla illo
doloremque voluptatum excepturi accusamus porro officiis tempore molestiae
saepe, iusto quibusdam explicabo obcaecati saepe quasi voluptate? Velit libero
tempore in nobis ratione nisi laborum rerum natus ipsam, aperiam placeat
laborum delectus dolor ab dolores itaque. Fuga maxime culpa quae adipisci, modi
quod distinctio ipsam, et vero natus consequuntur neque placeat saepe quam
perferendis, voluptate nemo ducimus ullam recusandae iusto laboriosam iure
temporibus sed saepe, optio dignissimos dolor modi accusamus quod culpa ab? Ad
dolore dignissimos, perferendis accusamus ducimus fuga eveniet a ut.

The code for this is on my GitHub.

Thu, 20 Nov 2025 15:00:00

John Benediktsson: Cardinal Direction

Cardinal direction describes points on a compass — North (N), East (E), South (S), and West (W).

In addition to those, there are also 4 intercardinal directions (Northwest or NW, NE, SW, SE), 8 secondary intercardinal directions (North-Northwest or NNW, WNW, NNE, ENE, WSW, SSW, ESE, SSE), as well as 16 tertiary intercardinal directions (Northwest-by-North or NWbN, etc.).

In fact, you can see all the points of the compass divided into 32 textual directions:

I like puzzles and sometimes those come from code golfing. I stumbled across two symmetric challenges on the Code Golf and Coding Challenges Stack Exchange:

I thought it would be a good task to code in Factor.

We start by enumerating the descriptive names for all 32 points of the compass. For convenience we use the quoted words vocabulary.

CONSTANT: directions qw{
    N NbE NNE NEbN NE NEbE ENE EbN
    E EbS ESE SEbE SE SEbS SSE SbE
    S SbW SSW SWbS SW SWbW WSW WbS
    W WbN WNW NWbW NW NWbN NNW NbW
}

Then, parsing a compass degrees to a textual name involves rounding to the nearest 32-point:

: compass>string ( compass -- str )
    360/32 / round >integer 32 mod directions nth ;

We can use some test cases from the challenges to check that it works:

{ "N"    } [ 0     compass>string ] unit-test
{ "NNE"  } [ 23.97 compass>string ] unit-test
{ "NEbN" } [ 33.7  compass>string ] unit-test
{ "ENE"  } [ 73.12 compass>string ] unit-test
{ "EbN"  } [ 73.13 compass>string ] unit-test
{ "SWbS" } [ 219   compass>string ] unit-test
{ "W"    } [ 275   compass>string ] unit-test
{ "WbN"  } [ 276   compass>string ] unit-test
{ "WNW"  } [ 287   compass>string ] unit-test

And the reverse converts the name back to compass degrees by grabbing the index and multiplying:

: string>compass ( str -- compass )
    directions index 360/32 * ;

It might not be the shortest solution, but it works and it was fun to build!

Wed, 19 Nov 2025 15:00:00

John Benediktsson: Flood Fill

Yesterday, Rodrigo Girão Serrão wrote an article about implementing the Floodfill algorithm in Python. He included a Javascript demonstration you can click on, as well as a step-by-step example at the end of his blog post to go over how flood fill works.

We are going to implement this in Factor and then extend the images.viewer vocabulary:

When working with bitmap pixel data, we typically store colors using integers in the range [0..255]. We can generate a random color with 4 bytes by simply using replicate:

:: random-color ( -- color )
    4 [ 255 random ] B{ } replicate-as ;

This allows us to implement the flood fill four-way algorithm:

Start from a specified pixel in an image.
Choose a random but different color to assign.
If the pixel is not the initial color, you’re done.
If the pixel is, then change it’s color.
For each surrounding pixel, continue from step 3.

CONSTANT: neighbors { { 1 0 } { 0 1 } { -1 0 } { 0 -1 } }

:: floodfill ( x y image -- ? )
    image dim>> first2 :> ( w h )
    {
        [ x 0 >= ] [ x w < ]
        [ y 0 >= ] [ y h < ]
    } 0&& [
        x y image pixel-at :> initial
        f [ drop random-color dup initial = ] loop :> color

        color x y image set-pixel-at
        V{ { x y } } :> queue

        [ queue empty? ] [
            queue pop first2 :> ( tx ty )
            neighbors [
                first2 :> ( dx dy )
                tx dx + :> nx
                ty dy + :> ny
                {
                    [ nx 0 >= ] [ nx w < ]
                    [ ny 0 >= ] [ ny h < ]
                    [ nx ny image pixel-at initial = ]
                } 0&& [
                    color nx ny image set-pixel-at
                    { nx ny } queue push
                ] when
            ] each
        ] until t
    ] [ f ] if ;

Note: as implemented, we change every pixel that matches the first click to a different color. It might be more aesthetic to allow for anti-aliasing to adjust colors that are fairly close to the original color.

Now, we’ll extend the image-gadget:

TUPLE: floodfill-gadget < image-gadget ;

: <floodfill-gadget> ( image -- gadget )
    floodfill-gadget new-image-gadget* ;

We implement a click handler that performs a flood fill and if it changed the image, cleans up the texture object and re-renders the gadget.

:: on-click ( gadget -- )
    gadget hand-rel first2 [ gl-scale >integer ] bi@ :> ( x y )
    x y gadget image>> floodfill [
        gadget delete-current-texture
        gadget relayout-1
    ] when ;

That word is assigned as a gesture on button-up mouse clicks:

floodfill-gadget "gestures" f {
    { T{ button-up { # 1 } } on-click }
} define-command-map

And, for convenience, make a main window word to launch the user interface with an example image:

MAIN-WINDOW: floodfill-window { { title "Floodfill" } }
    "vocab:floodfill/logo.png" <floodfill-gadget> >>gadgets ;

This is available on my GitHub.

Tue, 18 Nov 2025 15:00:00

John Benediktsson: Parsing Chemistry

In Python, the chemparse project is available as a “lightweight package for parsing chemical formula strings into python dictionaries” mapping chemical elements to numeric counts.

It supports parsing several variants of formula such as:

simple formulas like "H2O"
fractional stoichiometry like "C1.5O3"
groups such as "(CH3)2"
nested groups such as "((CH3)2)3"
square brackets such as "K4[Fe(SCN)6]"

I thought it would fun to build a similar functionality using Factor.

We are going to be using the EBNF syntax support to more simply write a parsing expression grammar. As is often the most useful way to implement things, we break it down into steps. We can parse a symbol as one or two letters, a number as an integer or float, and then a pair which is a symbol with an optional number prefix and postfix.

EBNF: split-formula [=[

symbol = [A-Z] [a-z]? => [[ sift >string ]]

number = [0-9]+ { "." [0-9]+ }? { { "e" | "E" } { "+" | "-" }? [0-9]+ }?

       => [[ first3 [ concat ] bi@ "" 3append-as string>number ]]

pair   = number? { symbol | "("~ pair+ ")"~ | "["~ pair+ "]"~ } number?

       => [[ first3 swapd [ 1 or ] bi@ * 2array ]]

pairs  = pair+

]=]

We can test that this works:

IN: scratchpad "H2O" split-formula .
V{ { "H" 2 } { "O" 1 } }

IN: scratchpad "(CH3)2" split-formula .
V{ { V{ { "C" 1 } { "H" 3 } } 2 } }

But we need to recursively flatten these into an assoc, mapping element to count.

: flatten-formula ( elt n assoc -- )
    [ [ first2 ] [ * ] bi* ] dip pick string?
    [ swapd at+ ] [ '[ _ _ flatten-formula ] each ] if ;

And combine those two steps to parse a formula:

: parse-formula ( str -- seq )
    split-formula H{ } clone [
        '[ 1 _ flatten-formula ] each
    ] keep ;

We can now test that this works with a few unit tests that show each of the features we hoped to support:

{ H{ { "H" 2 } { "O" 1 } } } [ "H2O" parse-formula ] unit-test

{ H{ { "C" 1.5 } { "O" 3 } } } [ "C1.5O3" parse-formula ] unit-test

{ H{ { "C" 2 } { "H" 6 } } } [ "(CH3)2" parse-formula ] unit-test

{ H{ { "C" 6 } { "H" 18 } } } [ "((CH3)2)3" parse-formula ] unit-test

{ H{ { "K" 4 } { "Fe" 1 } { "S" 6 } { "C" 6 } { "N" 6 } } }
[ "K4[Fe(SCN)6]" parse-formula ] unit-test

This is available in my GitHub.

Fri, 24 Oct 2025 15:00:00

John Benediktsson: Split Lines

William Woodruff recently noticed that Python’s splitlines does a lot more than just newlines:

I always assumed that Python’s str.splitlines() split strings by “universal newlines”, i.e., \n, \r, and \r\n.

But it turns out it does a lot more than that.

The recent Factor 0.100 release included a change to make the split-lines word split on unicode linebreaks which matches the Python behavior.

IN: scratchpad "line1\nline2\rline3\r\nline4\vline5\x1dhello"
               split-lines .
{ "line1" "line2" "line3" "line4" "line5" "hello" }

These are considered line breaks:

Character	Description
`\n`	Line Feed
`\r`	Carriage Return
`\r\n`	Carriage Return + Line Feed
`\v`	Line Tabulation
`\f`	Form Feed
`\x1c`	File Separator
`\x1d`	Group Separator
`\x1e`	Record Separator
`\x85`	Next Line (C1 Control Code)
`\u002028`	Line Separator
`\u002029`	Paragraph Separator

This might be surprising – or just what you needed!

Sun, 12 Oct 2025 15:00:00

John Benediktsson: Extensible Data Notation

I wrote about the Data Formats support that comes included in Factor. As I mentioned in that post, there are many more that we could implement. One of those is Extensible Data Notation – also known as EDN – and comes from the Clojure community.

We can see a nice example of the EDN format in Learn EDN in Y minutes:

; Comments start with a semicolon.
; Anything after the semicolon is ignored.

;;;;;;;;;;;;;;;;;;;
;;; Basic Types ;;;
;;;;;;;;;;;;;;;;;;;

nil         ; also known in other languages as null

; Booleans
true
false

; Strings are enclosed in double quotes
"hungarian breakfast"
"farmer's cheesy omelette"

; Characters are preceded by backslashes
\g \r \a \c \e

; Keywords start with a colon. They behave like enums. Kind of
; like symbols in Ruby.
:eggs
:cheese
:olives

; Symbols are used to represent identifiers. 
; You can namespace symbols by using /. Whatever precedes / is
; the namespace of the symbol.
spoon
kitchen/spoon ; not the same as spoon
kitchen/fork
github/fork   ; you can't eat with this

; Integers and floats
42
3.14159

; Lists are sequences of values
(:bun :beef-patty 9 "yum!")

; Vectors allow random access
[:gelato 1 2 -2]

; Maps are associative data structures that associate the key with its value
{:eggs        2
 :lemon-juice 3.5
 :butter      1}

; You're not restricted to using keywords as keys
{[1 2 3 4] "tell the people what she wore",
 [5 6 7 8] "the more you see the more you hate"}

; You may use commas for readability. They are treated as whitespace.

; Sets are collections that contain unique elements.
#{:a :b 88 "huat"}

;;;;;;;;;;;;;;;;;;;;;;;
;;; Tagged Elements ;;;
;;;;;;;;;;;;;;;;;;;;;;;

; EDN can be extended by tagging elements with # symbols.

#MyYelpClone/MenuItem {:name "eggs-benedict" :rating 10}

Recently, I implemented support for EDN, originally using Parsing Expression Grammar to do the parsing, and then adding support for encoding Factor objects into EDN, and then switching to a faster stream-based parsing approach.

This now allows us to parse that example above into:

{
    null
    t
    f
    "hungarian breakfast"
    "farmer's cheesy omelette"
    103
    114
    97
    99
    101
    T{ keyword { name "eggs" } }
    T{ keyword { name "cheese" } }
    T{ keyword { name "olives" } }
    T{ symbol { name "spoon" } }
    T{ symbol { name "kitchen/spoon" } }
    T{ symbol { name "kitchen/fork" } }
    T{ symbol { name "github/fork" } }
    42
    3.14159
    {
        T{ keyword { name "bun" } }
        T{ keyword { name "beef-patty" } }
        9
        "yum!"
    }
    V{
        T{ keyword { name "gelato" } }
        1
        2
        -2
    }
    LH{
        { T{ keyword { name "eggs" } } 2 }
        { T{ keyword { name "lemon-juice" } } 3.5 }
        { T{ keyword { name "butter" } } 1 }
    }
    LH{
        { V{ 1 2 3 4 } "tell the people what she wore" }
        { V{ 5 6 7 8 } "the more you see the more you hate" }
    }
    HS{
        88
        T{ keyword { name "a" } }
        T{ keyword { name "b" } }
        "huat"
    }
    T{ tagged
        { name "MyYelpClone/MenuItem" }
        { value
            LH{
                { T{ keyword { name "name" } } "eggs-benedict" }
                { T{ keyword { name "rating" } } 10 }
            }
        }
    }
}

The edn vocabulary is now included in the Factor standard library.

You can see some information about the various words currently available:

IN: scratchpad "edn" help
Extensible Data Notation (EDN)

The edn vocabulary supports reading and writing from the Extensible Data
Notation (EDN) format.

Reading from EDN:
 read-edns ( -- objects )
 read-edn ( -- object )
 edn> ( string -- objects )

Writing into EDN:
 write-edns ( objects -- )
 write-edn ( object -- )
 >edn ( object -- string )

Basic support is included for encoding Factor objects:

IN: scratchpad TUPLE: foo a b c ;

IN: scratchpad 1 2 3 foo boa write-edn
#scratchpad/foo {:a 1, :b 2, :c 3}

But we don’t automatically parse these tagged objects back into a Factor object at the moment.

Check it out!

Sun, 5 Oct 2025 15:00:00

[ planet-factor ]

Blogroll