[ planet-factor ]
John Benediktsson: Command Arguments
A question was asked recently on the Factor mailing list about the Argument Parser that I had previously implemented in Factor:
I have been trying to hack on command-line.parser to add the ability to call it with commands.
The specific feature they want is similar to the ArgumentParser.add_subparsers function in Python’s argparse module. I spent a little bit of time thinking about a quick implementation that can get us started, and applied this patch to support commands.
Here’s their example of a MAIN with two commands with different options using with-commands:
MAIN: [
H{
{
"add"
{
T{ option
{ name "a" }
{ type integer }
{ #args 1 }
}
}
}
{
"subtract"
{
T{ option
{ name "s" }
{ type integer }
{ #args 1 }
}
}
}
} [ ] with-commands
]
We currently produce no output by default when no command is specified:
$ ./factor foo.factor
The default help prints the possible commands:
$ ./factor foo.factor --help
Usage:
factor foo.factor [--help] [command]
Arguments:
command {add,subtract}
Options:
--help show this help and exit
Or get default help for a command:
$ ./factor foo.factor add --help
Usage:
factor foo.factor add [--help] [a]
Arguments:
a
Options:
--help show this help and exit
Or print an error if the argument is not a valid command:
$ ./factor foo.factor multiply
ERROR: Invalid value 'multiply' for option 'command'
There are other features we might want to add to this including per-command
metadata with a brief description of the command, support for additional
top-level options besides just the command, and perhaps a different way of
handling the no command case rather than empty output.
This is available in the latest developer version!
John Benediktsson: Fibonacci Style
About 14 years ago, I wrote about Fibonacci Wars which described the relative performance of three different methods of calculating Fibonacci numbers. Today, I wanted to address a style question that someone in the Factor Discord server asked:
How could I write this better?
: fib ( n -- f(n) ) 0 1 rot 1 - [ tuck + ] times nip ;In a more concatenative style.
I’ve written before about conciseness, concatenative thinking and readability. I found this question to be a good prompt that provides another opportunity to address these topics.
Their suggested solution is an iterative one and is fairly minimal when it comes to “short code”. It uses less common shuffle words like tuck that users might not understand easily. It is probably true that even rot is more inscrutable to people coming from other languages.
Let’s look at some potential variations!
You could use simpler stack shuffling:
: fib ( n -- f(n) )
[ 1 0 ] dip 1 - [ over + swap ] times drop ;
You could factor out the inner logic to another word:
: fib+ ( f(n-2) f(n-1) -- f(n-1) f(n) )
[ + ] keep swap ;
: fib ( n -- f(n) )
[ 0 1 ] dip 1 - [ fib+ ] times nip ;
You could use higher-level words like keepd:
: fib ( n -- f(n) )
[ 1 0 ] dip 1 - [ [ + ] keepd ] times drop ;
You could use locals and use index 0 as the “first” fib number:
:: fib ( n -- f(n) )
1 0 n [ [ + ] keepd ] times drop ;
You could write a recursive solution using memoization for improved performance:
MEMO: fib ( n -- f(n) )
dup 2 < [ drop 1 ] [ [ 2 - fib ] [ 1 - fib ] bi + ] if ;
You could use local variables to make it look nicer:
MEMO:: fib ( n -- f(n) )
n 2 < [ 1 ] [ n 2 - fib n 1 - fib + ] if ;
But, in many cases, beauty is in the eye of the beholder. And so you could start at a place where you find the code most readable, and that might even be something more conventional looking like this version that uses mutable locals and comments and whitespace to describe what is happening:
:: fib ( n -- f(n) )
0 :> f(n-1)!
1 :> f(n)!
! loop to calculate
n [
! compute the next number
f(n-1) f(n) + :> f(n+1)
! save the previous
f(n) f(n-1)!
! save the next
f(n+1) f(n)!
] times
! return the result
f(n) ;
Are any of these clearly better than the original version?
Are there other variations we should consider?
There are often multiple competing priorities when improving code style – including readability, performance, simplicity, and aesthetics. I encourage everyone to spend some time iterating on these various axes as they learn more about Factor!
John Benediktsson: Jaro-Winkler
Jaro-Winkler distance is a measure of string similarity and edit distance between two sequences:
The higher the Jaro–Winkler distance for two strings is, the less similar the strings are. The score is normalized such that 0 means an exact match and 1 means there is no similarity. The original paper actually defined the metric in terms of similarity, so the distance is defined as the inversion of that value (distance = 1 − similarity).
There are actually two different concepts – and RosettaCode tasks – implied by this algorithm:
- Jaro similarity and Jaro distance
- Jaro-Winkler similarity and Jaro-Winkler distance.
Let’s build an implementation of these in Factor!
Jaro Similarity
The base that all of these are built upon is the Jaro similarity. It is
calculated as a score by measuring the number of matches (m) between the
strings, counting the number of transpositions divided by 2 (t), and then returning a
weighted score using the formula using the lengths of each sequence (|s1|
and |s2|):
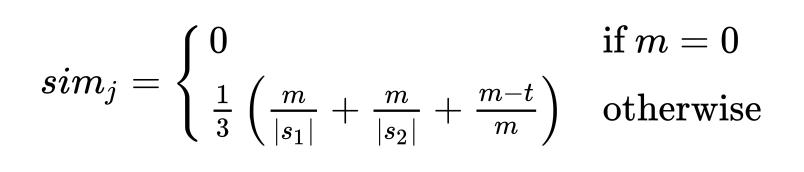
In particular, it considers a matching character to be one that is found in the other string within a match distance away, calculated by the formula:
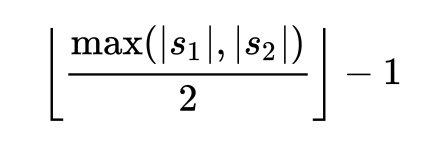
There are multiple ways to go about this, with varying performance, but I decided one longer function was simpler to understand than breaking out the steps into their own words. We use a bit-array to efficiently track which characters have been matched already as we iterate:
:: jaro-similarity ( s1 s2 -- n )
s1 s2 [ length ] bi@ :> ( len1 len2 )
len1 len2 max 2/ 1 [-] :> delta
len2 <bit-array> :> flags
s1 [| ch i |
i delta [-] :> from
i delta + 1 + len2 min :> to
from to [| j |
j flags nth [ f ] [
ch j s2 nth = dup j flags set-nth
] if
] find-integer-from
] filter-index
[ 0 ] [
[ length ] keep s2 flags [ nip ] 2filter [ = not ] 2count
:> ( #matches #transpositions )
#matches len1 /f #matches len2 /f +
#matches #transpositions 2/ - #matches /f + 3 /
] if-empty ;
The Jaro distance is then just a subtraction:
: jaro-distance ( s1 s2 -- n )
jaro-similarity 1.0 swap - ;
I’m curious if anyone else has a simpler implementation – please share!
Jaro-Winkler Similarity
The Jaro-Winkler similarity builds upon this by factoring in the length of
the common prefix (l) times a constant scaling factor (p) that is
usually set to 0.1 in most implementations I’ve seen:
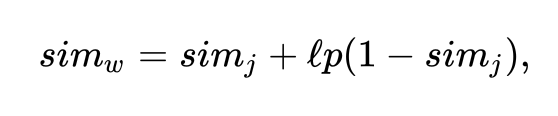
We can implement this by calcuting the Jaro similarity and then computing the common prefix and then generating the result:
:: jaro-winkler-similarity ( s1 s2 -- n )
s1 s2 jaro-similarity :> jaro
s1 s2 min-length 4 min :> len
s1 s2 [ len head-slice ] bi@ [ = ] 2count :> #common
1 jaro - #common 0.1 * * jaro + ;
The Jaro-Winkler distance is again just a subtraction:
: jaro-winkler-distance ( a b -- n )
jaro-winkler-similarity 1.0 swap - ;
Try it out
The Wikipedia article
compares the similarity of FARMVILLE and FAREMVIEL:
IN: scratchpad "FARMVILLE" "FAREMVIEL" jaro-similarity .
0.8842592592592592
We can also see that the algorithm considers the transposition of two close characters to be less of a penalty than the transposition of two characters farther away from each other. It also penalizes additions and substitutions of characters that cannot be expressed as transpositions.
IN: scratchpad "My string" "My tsring" jaro-winkler-similarity .
0.9740740740740741
IN: scratchpad "My string" "My ntrisg" jaro-winkler-similarity .
0.8962962962962963
We can compare the rough performance of Julia using the same algorithm:
julia> using Random
julia> s = randstring(10_000)
julia> t = randstring(10_000)
julia> @time jarowinklerdistance(s, t)
1.492011 seconds (108.32 M allocations: 2.178 GiB, 1.87% gc time)
0.19016926812348256
Note: I’m not a Julia developer, I just play one on
TV. I adapted this
implementation in
Julia, which
originally took over 4.5 seconds. A better developer could probably improve it
quite a bit. In fact, it was pointed out that we are indexing UTF-8 String
in a loop, and should instead collect the Char into a Vector first.
That does indeed make it super fast.
To the implementation in Factor that we built above, which runs quite a bit faster:
IN: scratchpad USE: random.data
IN: scratchpad 10,000 random-string
10,000 random-string
gc [ jaro-winkler-distance ] time .
Running time: 0.259643166 seconds
0.1952856823031448
Thats not bad for a first version that uses safe indexing with unnecessary bounds-checking, generic iteration on integers when usually the indices are fixnum (something I hope to fix someday automatically), and should probably order the input sequences by length for consistency.
If we fix those problems, it gets even faster:
IN: scratchpad USE: random.data
IN: scratchpad 10,000 random-string
10,000 random-string
gc [ jaro-winkler-distance ] time .
Running time: 0.068086625 seconds
0.19297898770334765
This is available in the development version in the math.similarity and the math.distances vocabularies.
John Benediktsson: Best Shuffle
The “Best shuffle” is a Rosetta Code task that was not yet implemented in Factor:
Task
Shuffle the characters of a string in such a way that as many of the character values are in a different position as possible.
A shuffle that produces a randomized result among the best choices is to be preferred. A deterministic approach that produces the same sequence every time is acceptable as an alternative.
Display the result as follows:
original string, shuffled string, (score)The score gives the number of positions whose character value did not change.
There are multiple ways to approach this problem, but the way that most solutions seem to take is to shuffle two sets of indices, and then iterate through them swapping the characters in the result if they are different.
I wanted to contribute a solution in Factor, using local variables and short-circuit combinators:
:: best-shuffle ( str -- str' )
str clone :> new-str
str length :> n
n <iota> >array randomize :> range1
n <iota> >array randomize :> range2
range1 [| i |
range2 [| j |
{
[ i j = ]
[ i new-str nth j new-str nth = ]
[ i str nth j new-str nth = ]
[ i new-str nth j str nth = ]
} 0|| [
i j new-str exchange
] unless
] each
] each
new-str ;
And we can write some code to display the result as requested:
: best-shuffle. ( str -- )
dup best-shuffle 2dup [ = ] 2count "%s, %s, (%d)\n" printf ;
And then print some test cases:
IN: scratchpad {
"abracadabra"
"seesaw"
"elk"
"grrrrrr"
"up"
"a"
} [ best-shuffle. ] each
abracadabra, raabaracdab, (0)
seesaw, easwse, (0)
elk, lke, (0)
grrrrrr, rrrrgrr, (5)
up, pu, (0)
a, a, (1)
This is reminiscent to the recent work I had done on derangements and generating a random derangement. While this approach does not generate a perfect derangement of the indices – and happens to be accidentally quadratic – it is somewhat similar with the additional step that we look to make sure not only are the indices different, but that the contents are different as well before swapping.
John Benediktsson: Dotenv
Dotenv is an informal file specification, a collection of implementations in different languages, and an organization providing cloud-hosting services. They describe the .env file format and some extensions:
The .env file format is central to good DSX and has been since it was introduced by Heroku in 2012 and popularized by the dotenv node module (and other libraries) in 2013.
The .env file format starts where the developer starts - in development. It is added to each project but NOT committed to source control. This gives the developer a single secure place to store sensitive application secrets.
Can you believe that prior to introducing the .env file, almost all developers stored their secrets as hardcoded strings in source control. That was only 10 years ago!
Besides official and many unofficial .env parsers available in a lot of
languages, the Dotenv
organization provides support for dotenv-vault
cloud services in Node.js, Python,
Ruby, Go, PHP, and Rust.
Today, I wanted to show how you might implement a .env parser in
Factor.
File Format
The .env files are relatively simple formats with key-value pairs that
are separated by an equal sign. These values can be un-quoted,
single-quoted, double-quoted, or backtick-quoted strings:
SIMPLE=xyz123
INTERPOLATED="Multiple\nLines"
NON_INTERPOLATED='raw text without variable interpolation'
MULTILINE = `long text here,
e.g. a private SSH key`
Parsing
There are a lot of ways to build a parser – everything from manually spinning through bytes using a hand-coded state machine, higher-level parsing grammars like PEG, or explicit parsing syntax forms like EBNF.
We are going to implement a .env parser using standard PEG parsers,
beginning with some parsers that look for whitespace, comment lines, and
newlines:
: ws ( -- parser )
[ " \t" member? ] satisfy repeat0 ;
: comment ( -- parser )
"#" token [ CHAR: \n = not ] satisfy repeat0 2seq hide ;
: newline ( -- parser )
"\n" token "\r\n" token 2choice ;
Keys
The .env keys are specified simply:
For the sake of portability (and sanity), environment variable names (keys) must consist solely of letters, digits, and the underscore ( _ ) and must not begin with a digit. In regex-speak, the names must match the following pattern:
[a-zA-Z_]+[a-zA-Z0-9_]*
We can build a key parser by looking for those characters:
: key-parser ( -- parser )
CHAR: A CHAR: Z range
CHAR: a CHAR: z range
[ CHAR: _ = ] satisfy 3choice
CHAR: A CHAR: Z range
CHAR: a CHAR: z range
CHAR: 0 CHAR: 9 range
[ CHAR: _ = ] satisfy 4choice repeat0
2seq [ first2 swap prefix "" like ] action ;
Values
The .env values can be un-quoted, single-quoted, double-quoted, or backtick-quoted strings. Only double-quoted strings support escape characters, but single-quoted and backtick-quoted strings support escaping either single-quotes or backtick characters.
: single-quote ( -- parser )
"\\" token hide [ "\\'" member? ] satisfy 2seq [ first ] action
[ CHAR: ' = not ] satisfy 2choice repeat0 "'" dup surrounded-by ;
: backtick ( -- parser )
"\\" token hide [ "\\`" member? ] satisfy 2seq [ first ] action
[ CHAR: ` = not ] satisfy 2choice repeat0 "`" dup surrounded-by ;
: double-quote ( -- parser )
"\\" token hide [ "\"\\befnrt" member? ] satisfy 2seq [ first escape ] action
[ CHAR: " = not ] satisfy 2choice repeat0 "\"" dup surrounded-by ;
: literal ( -- parser )
[ " \t\r\n" member? not ] satisfy repeat0 ;
Before we implement our value parser, we should note that some values can be interpolated:
Interpolation (also known as variable expansion) is supported in environment files. Interpolation is applied for unquoted and double-quoted values. Both braced (
${VAR}) and unbraced ($VAR) expressions are supported.Direct interpolation
${VAR}-> value of VARDefault value
${VAR:-default}-> value ofVARif set and non-empty, otherwise default${VAR-default}-> value ofVARif set, otherwise default
And some values can have command substitution:
Add the output of a command to one of your variables in your .env file. Command substitution is applied for unquoted and double-quoted values.
Direct substitution
$(whoami)-> value of$ whoami
We can implement an interpolate parser that acts on strings and replaces observed variables with their interpolated or command-substituted values. This uses a regular expressions and re-replace-with to substitute values appropriately.
: interpolate-value ( string -- string' )
R/ \$\([^)]+\)|\$\{[^\}:-]+(:?-[^\}]*)?\}|\$[^(^{].+/ [
"$(" ?head [
")" ?tail drop process-contents [ blank? ] trim
] [
"${" ?head [ "}" ?tail drop ] [ "$" ?head drop ] if
":-" split1 [
[ os-env [ empty? not ] keep ] dip ?
] [
"-" split1 [ [ os-env ] dip or ] [ os-env ] if*
] if*
] if
] re-replace-with ;
: interpolate ( parser -- parser )
[ "" like interpolate-value ] action ;
We can use that to build a value parser, remembering that only un-quoted and double-quoted values are interpolated, and making sure to convert the result to a string:
: value-parser ( -- parser )
[
single-quote ,
double-quote interpolate ,
backtick ,
literal interpolate ,
] choice* [ "" like ] action ;
Key-Values
Combining those, we can make a key-value parser, that ignores whitespace
around the = token and uses
set-os-env
to update the environment
variables:
: key-value-parser ( -- parser )
[
key-parser ,
ws hide ,
"=" token hide ,
ws hide ,
value-parser ,
] seq* [ first2 swap set-os-env ignore ] action ;
And finally, we can build a parsing word that looks for these key-value pairs while ignoring optional comments and whitespace:
PEG: parse-dotenv ( string -- ast )
ws hide key-value-parser optional
ws hide comment optional hide 4seq
newline list-of hide ;
Loading Files
We can load a file by reading the file-contents and then parsing it into environment variables:
: load-dotenv-file ( path -- )
utf8 file-contents parse-dotenv drop ;
These .env files are usually located somewhere above the current directory,
typically at a project root. For now, we make a word that traverses from the
current directory up to the root, looking for the first .env file that
exists:
: find-dotenv-file ( -- path/f )
f current-directory get absolute-path [
nip
[ ".env" append-path dup file-exists? [ drop f ] unless ]
[ ?parent-directory ] bi over [ f ] [ dup ] if
] loop drop ;
And now, finally, we can find and then load the relevant .env file, if
there is one:
: load-dotenv ( -- )
find-dotenv-file [ load-dotenv-file ] when* ;
Try it out
We can make a simple .env file:
$ cat .env
HOST="${HOST:-localhost}"
PORT="${PORT:-80}"
URL="https://${HOST}:${PORT}/index.html"
And then try it out, overriding the PORT environment variable:
$ PORT=8080 ./factor
IN: scratchpad USE: dotenv
IN: scratchpad load-dotenv
IN: scratchpad "URL" os-env .
"https://localhost:8080/index.html"
Some additional features that we might want to follow up on:
- investigate the POSIX-compliant dotenv syntax specification and included test cases
- optionally use a startup
hook
to automatically load
.envfiles - support for dotenv-vaults and encrypted deploys
- command-line support similar to dotenvx
This is available in the latest development version. Check it out!
John Benediktsson: Color Prettyprint
Factor has a neat feature in the prettyprint
vocabulary
that allows printing objects, typically as valid source literal expressions.
There are small caveats to that regarding circularity, depth limits, and
other prettyprint control
variables,
but it’s roughly true that you can pprint most everything and have it be
useful.
At some point in the past few years, I noticed that Xcode and Swift Playground have support for color literals that are rendered in the source code. You can see that in this short video describing how it works:
Inspired by that – and a past effort at color tab completion – I thought it would be fun to show how you might extend our color support to allow colors to be prettyprinted with a little gadget in the UI that renders their colors.
First, we need to define a section object that holds a color and renders it using a colored border gadget.
TUPLE: color-section < section color ;
: <color-section> ( color -- color-section )
1 color-section new-section swap >>color ;
M: color-section short-section
" " <label> { 5 0 } <border>
swap color>> <solid> >>interior
COLOR: black <solid> >>boundary
output-stream get write-gadget ;
Next, we extend pprint* with a custom implementation for any color type
as well as our named
colors
that adds a color section to the output block:
M: color pprint*
<block
[ call-next-method ]
[ <color-section> add-section ] bi
block> ;
M: parsed-color pprint*
<block
[ \ COLOR: pprint-word string>> text ]
[ <color-section> add-section ] bi
block> ;
And, now that we have that, we can push some different colors to the stack and see how they are all displayed:

Pretty cool.
I did not commit this yet – partly because I’m not sure we want this as-is and also partly because it needs to only display the gadget if the UI is running. We also might want to consider the UI theme and choose a nice contrasting color for the border element.
John Benediktsson: Tracking Dict
Peter Bengtsson wrote about building a Python dict that can report which keys you did not use:
This can come in handy if you’re working with large Python objects and you want to be certain that you’re either unit testing everything you retrieve or certain that all the data you draw from a database is actually used in a report.
For example, you might have a
SELECT fieldX, fieldY, fieldZ FROM ...SQL query, but in the report you only usefieldX, fieldYin your CSV export.class TrackingDict(dict): def __init__(self, *args, **kwargs): super().__init__(*args, **kwargs) self._accessed_keys = set() def __getitem__(self, key): self._accessed_keys.add(key) return super().__getitem__(key) @property def accessed_keys(self): return self._accessed_keys @property def never_accessed_keys(self): return set(self.keys()) - self._accessed_keys
We can build a version of this in Factor intended to show off a few language features. The original version in Python used inheritance versus composition to implement the data structure. Instead, we build a data structure that will wrap an existing assoc and delegate to it.
First, a simple tuple definition that will have the underlying assoc and a set of accessed keys:
TUPLE: tracking-assoc underlying accessed-keys ;
: <tracking-assoc> ( underlying -- tracking-assoc )
HS{ } clone tracking-assoc boa ;
INSTANCE: tracking-assoc assoc
We then implement the assoc protocol by using delegation to the underlying assoc, with an override for tracking accessed keys:
CONSULT: assoc-protocol tracking-assoc underlying>> ;
M: tracking-assoc at*
[ underlying>> at* ] [ accessed-keys>> adjoin ] 2bi ;
And for fun – since we could have built a normal word to do this – we define a protocol slot that we then implement to compute the never accessed keys:
SLOT: never-accessed-keys
M: tracking-assoc never-accessed-keys>>
[ underlying>> keys ] [ accessed-keys>> ] bi diff ;
And we show it works using a simple example from the original blog post:
H{
{ "name" "John Doe" }
{ "age" 30 }
{ "email" "jd@example.com" }
} <tracking-assoc>
"name" over at "John Doe" assert=
[ accessed-keys>> "Accessed keys: %u\n" printf ]
[ never-accessed-keys>> "Never accessed keys: %u\n" printf ] bi
Which prints this:
Accessed keys: HS{ "name" }
Never accessed keys: HS{ "email" "age" }
Fun!
John Benediktsson: bab=aaa, bbb=bb
Admittedly, I struggle sometimes when I read the word “monoid”. It seems to always remind me of that saying “A Monad is just a Monoid in the Category of Endofunctors” which is both a tongue-twister, requires repeated effort to understand, and is sometimes used in casual conversation when jealously describing the features and capabilities of the Haskell programming language.
In any event, the topic of monoids came up recently on the Factor Discord server. Slava Pestov, the original creator of the Factor programming language, was describing recent work he was doing on some fun mathematical problems:
I’m searching for examples of finitely-presented monoids that cannot be presented by finite complete rewriting systems:
- ⟨a, b | aba=aa, baa=aab⟩ – my first result in this space.
- ⟨a, b | bab=aaa, bbb=bb⟩ – explore the equivalence class of a8 in this remarkable monoid.
He clarified in the discussion that “the Knuth-Bendix algorithm can solve many cases but not these two, which is how I found them in the first place”.
The second link above – made extra fun because it uses a=🍎 and b=🍌
to make a more emojiful experience – describes this specific problem in more
detail and presents it as a simple game to play. You can see the available
rules, the current state, and the next possible states achieved by applying
either of the rules, which are bi-directional.
Your pie recipe calls for 10 apples, but you only have 8 apples.
Can you turn your 8 apples into 10 apples with these two magic spells?
- 🍌🍎🍌 ↔️ 🍎🍎🍎
- 🍌🍌🍌 ↔️ 🍌🍌
Current state:
🍎🍎🍎🍎🍎🍎🍎🍎
Tap to cast a spell:
- 🍌🍎🍌🍎🍎🍎🍎🍎
- 🍎🍌🍎🍌🍎🍎🍎🍎
- 🍎🍎🍌🍎🍌🍎🍎🍎
- 🍎🍎🍎🍌🍎🍌🍎🍎
- 🍎🍎🍎🍎🍌🍎🍌🍎
- 🍎🍎🍎🍎🍎🍌🍎🍌
When exploring things like this, many questions come to mind. For example:
- Is this even solvable?
- What is the shortest solution?
- How many short solutions exist?
- How many of the possible states lead to the solution?
- How large is the set of all possible states?
After the link was shared, I must have clicked through about 5000 different state transitions hoping to randomly stumble upon the solution. And, eventually, recognized that it might be a good idea – or even possibly poetic – to do that exploration using Factor.
Warning: Spoilers ahead!
Let’s start by writing the rules:
CONSTANT: rules {
{ "bab" "aaa" }
{ "bbb" "bb" }
}
For convenience, we will make a sequence containing all the rules – since these are bi-directional and can be applied in either direction – using a literal expression.
CONSTANT: all-rules $[
rules dup [ swap ] assoc-map append
]
We can make a word that takes a from node and applies a
quotation to the
result of rules a -> b. Notice that we’re able to use our previous work on
finding subsequences:
:: each-move ( from a b quot: ( next -- ) -- )
from dup a subseq-indices [
cut a length tail b glue quot call
] with each ; inline
And then a word that returns all the next states:
: all-moves ( from -- moves )
[ all-rules [ first2 [ , ] each-move ] with each ] { } make ;
It’s often good practice to try each step out during development, so let’s do that and show the first six possible next states match the ones from the game:
IN: scratchpad "aaaaaaaa" all-moves .
{
"babaaaaa"
"ababaaaa"
"aababaaa"
"aaababaa"
"aaaababa"
"aaaaabab"
}
The next state is nice to have, but we’re generally going to be accumulating paths which are a series of states achieved by traversing the graph of all possible states:
:: all-paths% ( path -- )
path last all-rules [
first2 [ path swap suffix , ] each-move
] with each ;
: all-paths ( paths -- paths' )
[ [ all-paths% ] each ] { } make members ;
So, these are the first two steps in traversing the graph. You can see that some of the possible second moves end up circling back to the starting position, which makes sense since the rules are bi-directional and if applied can be un-applied on the next step.
IN: scratchpad { { "aaaaaaaa" } } all-paths dup . nl all-paths .
{
{ "aaaaaaaa" "babaaaaa" }
{ "aaaaaaaa" "ababaaaa" }
{ "aaaaaaaa" "aababaaa" }
{ "aaaaaaaa" "aaababaa" }
{ "aaaaaaaa" "aaaababa" }
{ "aaaaaaaa" "aaaaabab" }
}
{
{ "aaaaaaaa" "babaaaaa" "aaaaaaaa" }
{ "aaaaaaaa" "babaaaaa" "babbabaa" }
{ "aaaaaaaa" "babaaaaa" "babababa" }
{ "aaaaaaaa" "babaaaaa" "babaabab" }
{ "aaaaaaaa" "ababaaaa" "aaaaaaaa" }
{ "aaaaaaaa" "ababaaaa" "ababbaba" }
{ "aaaaaaaa" "ababaaaa" "abababab" }
{ "aaaaaaaa" "aababaaa" "aaaaaaaa" }
{ "aaaaaaaa" "aababaaa" "aababbab" }
{ "aaaaaaaa" "aaababaa" "aaaaaaaa" }
{ "aaaaaaaa" "aaababaa" "babbabaa" }
{ "aaaaaaaa" "aaaababa" "aaaaaaaa" }
{ "aaaaaaaa" "aaaababa" "babababa" }
{ "aaaaaaaa" "aaaababa" "ababbaba" }
{ "aaaaaaaa" "aaaaabab" "aaaaaaaa" }
{ "aaaaaaaa" "aaaaabab" "babaabab" }
{ "aaaaaaaa" "aaaaabab" "abababab" }
{ "aaaaaaaa" "aaaaabab" "aababbab" }
}
Let’s solve for the shortest paths, we keep track of states we’ve previously seen to avoid cycles, and we iterate using breadth-first-search until we find any solutions:
:: shortest-paths ( from to -- moves )
HS{ from } clone :> seen
{ { from } } :> stack!
f [
drop
! find all next possibilities
stack all-paths
! reject ones that circle back to visited nodes
[ last seen in? ] reject
! reject any that are over the length of ``to``
to length '[ last length _ > ] reject stack!
! add the newly visited nodes
stack [ last seen adjoin ] each
! stop when we find any solutions
stack [ last to = ] filter dup empty?
] loop ;
Note: we reject any states that are longer than our goal state. This provides a nice way to cull the graph and make the search performance more reasonable. You could also choose not do that, and exhaustively search into that area. However, while this is not generally a valid approach to solving these types of problems, it is specifically a valid approach to this one.
There are quite a few shortest paths:
IN: scratchpad "aaaaaaaa" "aaaaaaaaaa" shortest-paths length .
560
Each of those contain 16 nodes, which means 15 rules were applied:
IN: scratchpad "aaaaaaaa" "aaaaaaaaaa" shortest-paths first length .
16
But they only go through a seemingly small number of nodes:
IN: scratchpad "aaaaaaaa" "aaaaaaaaaa" shortest-paths concat members length .
43
How many nodes are there in total in the graph? Let’s find out!
:: full-graph ( from to -- seen )
HS{ from } clone :> seen
{ { from } } [
! find all next possibilities
all-paths
! reject any that are over the length of ``to``
to length '[ last length _ > ] reject
! only include ones that visit new nodes
[ last seen ?adjoin ] filter
] until-empty seen ;
We can see that the shortest solutions go through about 15% of the nodes:
IN: scratchpad "aaaaaaaa" "aaaaaaaaaa" full-graph cardinality .
279
We can use our graph traversal approach and Graphviz to visualize where solutions are found, showing how some areas of the graph are quite hard to randomly get out of and then on the correct path to a solution. We draw the starting node green, the ending node blue, and the nodes that involved in the shortest path as gray:
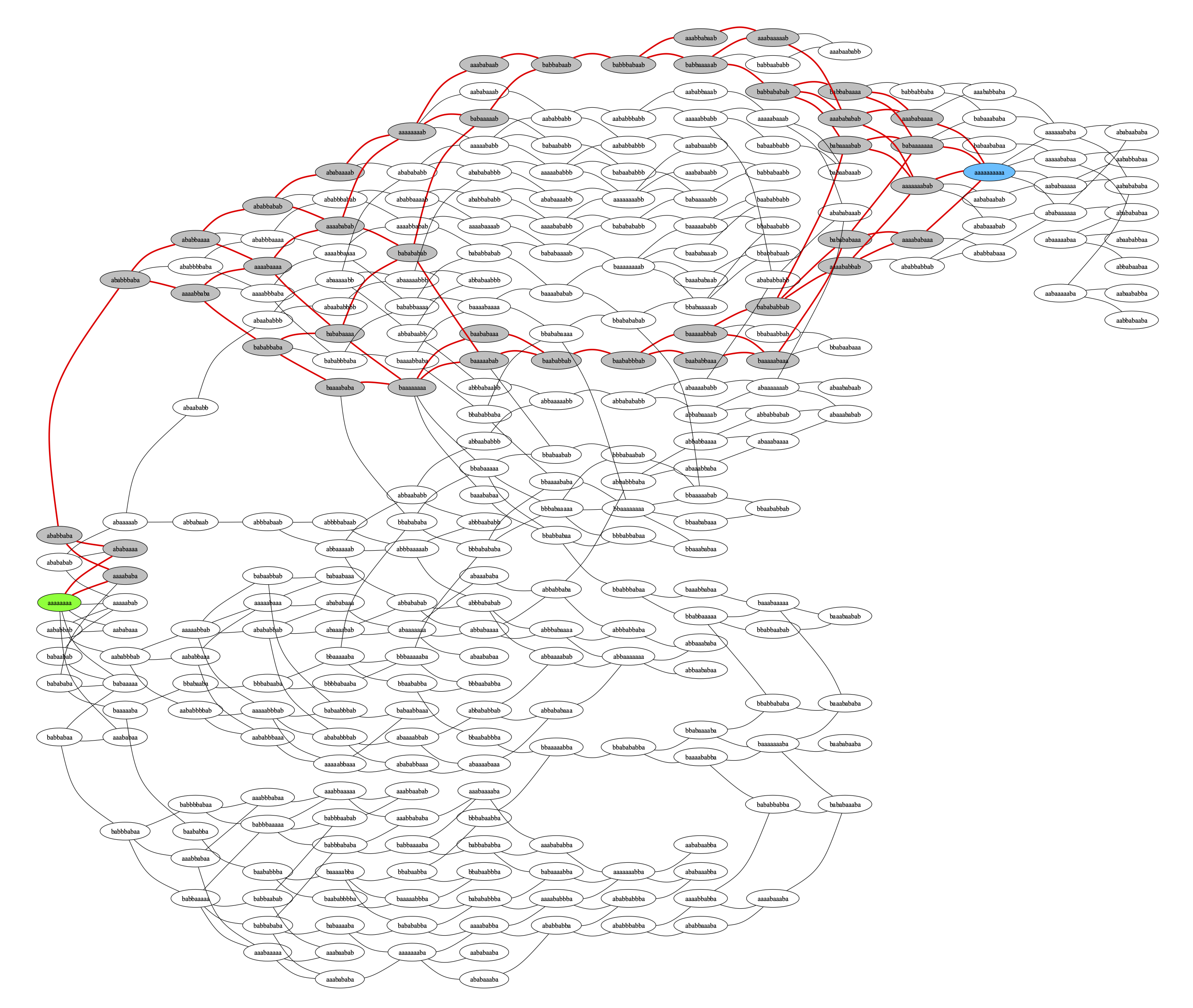
And that’s kind of interesting, but if we cluster nodes by their depth when first discovered, some other patterns show up:
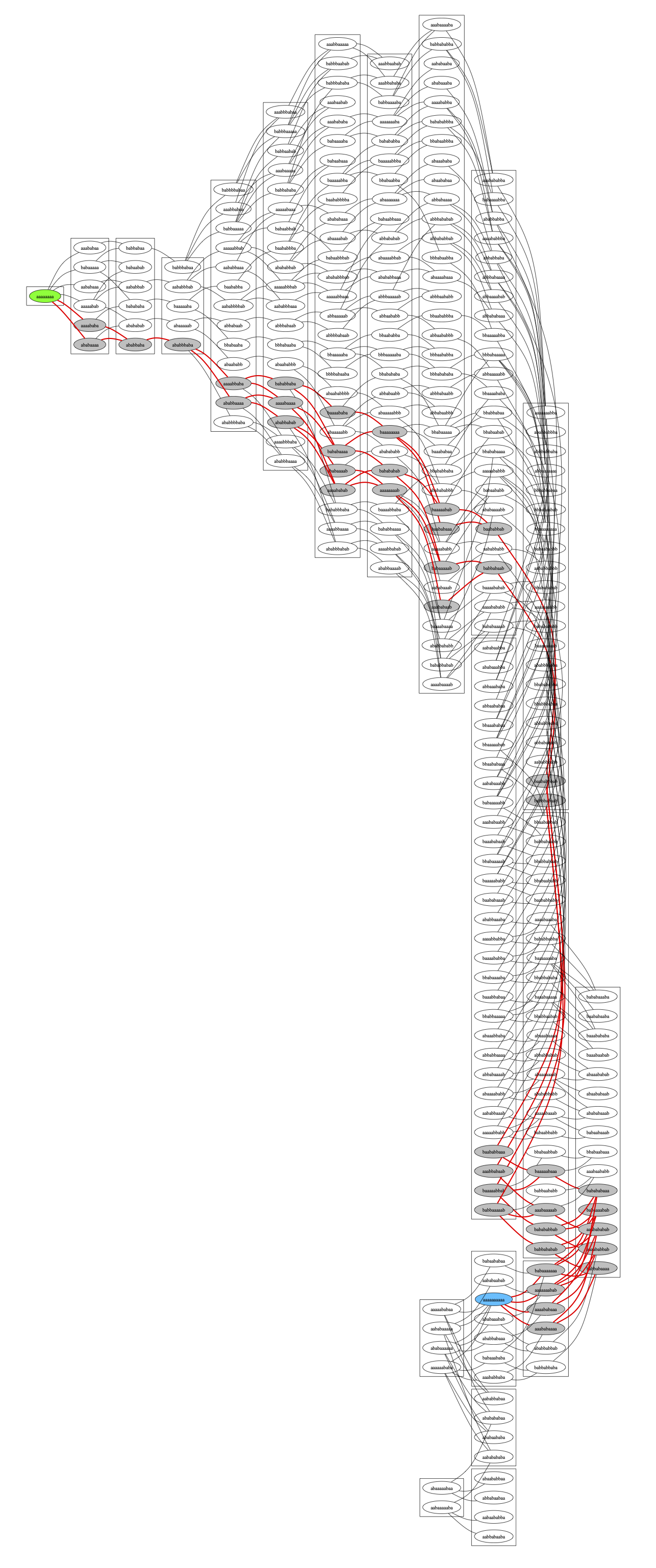
Such a fun problem!
Blogroll
- Chris Double
- Daniel Ehrenberg
- Doug Coleman
- Jeremy Hughes
- Joe Groff
- John Benediktsson
- Phil Dawes
- Samuel Tardieu
- Slava Pestov
planet-factor is an Atom/RSS aggregator that collects the contents of Factor-related blogs. It is inspired by Planet Lisp.